A Revolution of Chinese
Calculators
================
HOW TO LEARN |
|---|
LEE'S ABACUS |
|---|
================
With Illustrations & Examples

By
Inventor: Lee Kai-chen
HOW TO LEARN
LEE'S ABACUS
With Illustrations & Examples
By
Inventor: Lee Kai-chen

Copyright, May, 1959 by LEE'S ABACUS CORRESPO-
NDENCE SCHOOL, House No. 10, Lane 103, South
Hsin-sheng Road, Section 1, Taipei, Taiwan, China.
All rights reserved. No part of this book may produced in
any form, by mimeograph or any other means, without written
permission from the author.
Printed in Taiwan, China
First Printing ......... June, 1958
Second Printing .... December, 1958
CONTENTS
Chapter Page
1. INTRODUCTION .......................... 1
2. ADDITION .............................. 5
3. SUBTRACTION ........................... 11
4. MULTIPLICATION ........................ 17
5. DIVISION .............................. 27
6. EXTRACTION OF SQUARE ROOTS ............ 43
7. EXTRACTION OF CUBIC ROOTS ............. 51
CHAPTER 1.
INTRODUCTION
1. Merits to the Lee's Improved Abacus
The Lee's IMPROVED abacus well claim to be the best
of all kinds of existing arithmometer, in that:
(1) It makes speedy calculation - The findings of the international
contests held in New York and Tokyo respectively in the year 1946
as well as the several contests held in Taipei in 1953 and 1956 have
established the fact that even the electric calculator is no match
to the abacus in solving arithmetical problems, let alone other cal-
culating devices.
(2) It is error proof - The very simple design of consistently assign-
ing the value 5 to each bead counter on the upper deck and the
value 1 to each bead counter on the lower deck, and the mechanical
procedures called for in carrying out the operations, preclude any
error derivable from either human or machine failures.
(3) It is easy for the beginner to learn - The notation system that
each rod stands for a definite digit and each bead counter, a
specific number, leaves no doubt whatsoever even in the mind of
the very beginner. Especially when one is to carry out the opera-
tions for multiplication and division, one can master the methods
employed on the Lee's IMPROVED abacus in a blink of an eye
provided that one has an understanding on the methods employed
in ordinary arithmetic, and do a much faster and better job than
to write down all the steps on paper, which often becomes very
tiresome, or to do it on the old-styled abacus which involves many
operations that deny direct reasoning.
(4) It is handily carriable - The whole thing weighs only 1 1/2
pound, and can be handled as easily as an ordinary office file-holder.
1
INTRODUCTION
(5) It is easy to operate on - Unlike operating a calculating
machine, which is necessarily heavy, one can lay the abacus on
ones lap and complete the desired calculations without using a
single sheet of paper or making a single stroke by the pencil, which
are indispensable in the ordinary arithmetic practices.
(6) It has beautiful cutlook and durable construction - The bead
counters are eye pleasing by themselves. They literally look as
cute as so many gems. the beautifully painted wooden frame is
extraordinarily durable. The Lee's abacus is, therefore, a valuable
instrument and treasurable ornament all in one.
(7) It is inexpensive - In spite of its multifarious merits, the Lee's
abacus is obtainable at so very low a price that even a schooling
teenager can afford to get one with his or her own pocket money.
2. Nomenclature
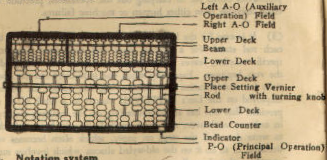
3. Notation system
Turn the place setting vernier to have the red dot fall between
any two rods. This done, the first rod to the left of the dot is
ready for registering all numbers from 0 to 9, the second rod is to its
2
INTRODUCTION
left is to be used for registering all digits of the order of tens, the
third rod to its left is to be used for registering all digits of the
order of hundreds, etc. The rods to the right of the dot are to be
used to register digits of the order of tenths, hundredths, thou-
sandths, etc.
To register any given number on the abacus, remember: Each
bead counter of the lower deck has the value 1, while each bead
counter of the upper deck has the value 5. The number register-
ed on the abacus in the above illustration should therefore read
12,345.6789.
The same notation system applies to both the left and the
right A-O fields as well.
4. The way to move the bead counters
To use the Lee's improved abacus property, it is essential to
aim at speed and accuracy. Remarkable skill can be attained if
the user is able to achieve coordination of his fingers, and his hand
and brain. Accuracy and speed largely depend on skillful manipula-
tion of the bead counters by the fingers.
To move the bead counters of the P-O field we generally use
the thumb, index finger or middle finger of the right hand. The
three fingers are used in the following way:
3
INTRODUCTION
(1) The thumb controls the movement of the lower bead counters
upwards to the beam.
(2) The index finger controls the movement of the lower bead
counters downwards away from the beam.
(3) The middle finger controls the movement of the upper bead
counters downwards to the beam, or away form the beam.
To move the bead counters of the left A-O field or the right
A-O field, we generally use the thumb or index finger of the right
hand. The two fingers are used in the following way:
(1) The thumb controls the movement of the lower bead counters
upwards to the beam.
(2) The index finger controls the movement of the lower bead
counters downwards away from the beam, and the upper bead
counters downwards to the beam, or away from the beam.
Thus the thumb and each finger have their own special work
to do. Naturally a learner may, at first, have to sacrifice speed for
the sake of accuracy as the latter is indispensable in the operation
of the Lee's improved abacus.
4
CHAPTER 2.
ADDITION
To make an addition on an abacus is simply to register the
numbers to be added one after another in accordance with the
notation system explained above, following a left-to-right direction
as when one writes down the Arabic figures. So long as all the digits
are correctly placed, the final reading should be the sum in question.
For all cases, the techniques involved in making additions are as
follows:
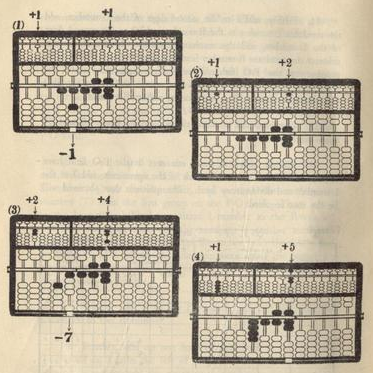
1. SIMPLE ADDING OF BEAD COUNTERS - This tech-
nique is used when, for instance, 6 is added to 2. In doing this,
all one need to do is to move down one bead counter of the upper
deck close to the beam and move another one bead counter of the
lower deck up to complete the operation of adding 6, which, together
with the two bead counters in the lower deck moved up to give the
number 2 before carrying out the operation for addition, auto-
matically shows the resultant sum 8.
| | | Operations Involved
Addition | Original number | Formula | Bead counter of | Bead counter of
| | | the lower deck | the upper deck
--------------------------------------------------------------------------
1 | 0,1,2,3,5,6,7,8. | 1 = +1 | +1 |
2 | 0,1,2,5,6,7. | 2 = +2 | +2 |
3 | 0,1,5,6. | 3 = +3 | +3 |
4 | 0,5. | 4 = +4 | +4 |
5 | 0,1,2,3,4. | 5 = +5 | | +1
6 | 0,1,2,3. | 6 = +6 | +1 | +1
7 | 0,1,2. | 7 = +7 | +2 | +1
8 | 0,1. | 8 = +8 | +3 | +1
9 | 0. | 9 = +9 | +4 | +1
Remarks: "+" represents the operation of moving the bead
counter(s) close to the beam.
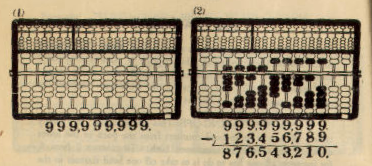
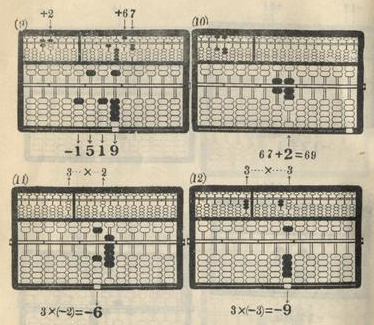
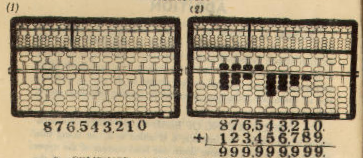
Example: 876,543,210 + 123,456,789 = 999,999,999
5
ADDITION
2. COMBINED ADDING-UP AND TAKING-OFF - This
technique is called for when the original number registered on a
rod is smaller than 5, but will become greater than 5 after the
addition is made. The question required is to move one bead
counter of the upper deck down to the beam and one or more bead
counters of the lower deck off the pack. For example, when 4 is
to be added to 3, the operation required is to move one bead counter
of the upper deck down to the beam and one bead counter off the
original 3, having only two bead counters in the pack of the lower
deck, which together with the one bead counter of the upper deck,
give the answer 7.
| | | Operations Involved
Addition | Original | Formula | Bead counter of | Bead counter of
| number | | the lower deck | the upper deck
--------------------------------------------------------------------
1 | 4. | 1 = +5-4 | -4 | +1
2 | 4,3. | 2 = +2-3 | -3 | +1
3 | 4,3,2. | 3 = +3-2 | -2 | +1
4 | 4,3,2,1. | 4 = +4-1 | -1 | +1
Remarks: "-" represents the operation of moving the bead
counter(s) off the beam.
6
ADDITION
Example: 1,234,444 + 4,321,432 = 5,555,876
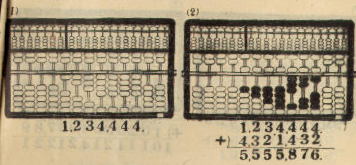
3. COMBINED TAKING-OFF AND PLACE ADVANCE-
MENT - This technique is called for when a sum greater than 10
occurs on a certain rod. The actual operation will then be to take
off bead counters of the lower deck, or the upper deck, or both,
and to add 1 on the rod to its left. The user may try to add 9 to
8 for practice.
| | | Operations Involved
| Original | |Bead counter|Bead counter|Bead counter of the
Addition| number |Formula| of the | of the | lower deck
| | | lower deck | upper deck |second to the left
-------------------------------------------------------------------------------
1 |9. |1=-9+10| -4 | -1 | +1
2 |8,9. |2=-8+10| -3 | -1 | +1
3 |7,8,9. |3=-7+10| -2 | -1 | +1
4 |6,7,8,9. |4=-6+10| -1 | -1 | +1
5 |5,6,7,8,9. |5=-5+10| | -1 | +1
6 |4,9. |6=-4+10| -4 | | +1
7 |3,4,8,9. |7=-3+10| -3 | | +1
8 |2,3,4,7,8,9. |8=-2+10| -2 | | +1
9 |1,2,3,4,6,7,8,9.|9=-1+10| -1 | | +1
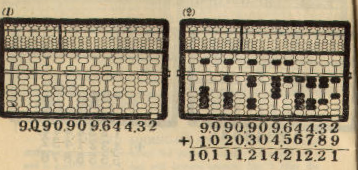
Example: 9,090,909,644.32 + 1,020,304,567.89 = 10,111,214,212.21
7
ADDITION
4. COMBINED ADDING-UP, TAKING-OFF AND
PLACE ADVANCEMENT - There are cases in which the actual
operation required consists of adding-up in the lower deck, taking-
off in the upper deck and again adding 1 on the rod for a higher
order. This technique is called for when, for instance, 6 is to be
added to 7.
| | | Operations Involved
|Original| |Bead counter|Bead counter|Bead counter of the
Addition| number | Formula | of the | of the | lower deck
| | | lower deck | upper deck |second to the left
----------------------------------------------------------------------------
6 |5,6,7,8.|6 = +1-5+10| +1 | -1 | +1
7 |5,6,7. |7 = +2-5+10| +2 | -1 | +1
8 |5,6. |8 = +3-5+10| +3 | -1 | +1
9 |5. |9 = +4-5+10| +4 | -1 | +1
8
ADDITION
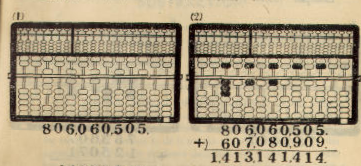
Example: 806,060,505 + 607,080,909 = 1,413,141,414
It has been found to be a much simpler and faster process to
make additions on an abacus than to do them on paper, especially
when there are many numbers to be added together.
The actual procedures can be shown as follows:
Original number
+) 1st addition
--------------------
1st sum
+) 2nd addition
--------------------
2nd sum
+) 3rd addition
--------------------
3rd sum
+) 4th addition
--------------------
..............
..............
..............
--------------------
(n-1)th sum
+) nth addition
--------------------
nth sum (Final result)
9
ADDITION
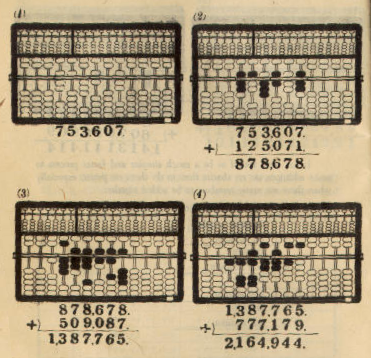
Example: 753,607+125,071 + 509,087+777,179 = 2,164,944
10
CHAPTER 3.
SUBTRACTION
To subtract one number from another, first register the minuend
on the abacus; then proceed to subtract place by place (rod by rod),
starting from the left. The final reading on the abacus should give
the answer required. For all cases, the techniques involved in
making subtractions are as follows:
1. SIMPLE TAKING-OFF - This is achieved by simply
taking off one or more bead counters from the pack in the lower
deck, or upper deck, or sometimes, both. To subtract 7 from 9,
for instance, all one has to do is to take off one bead counter in the
upper deck and two in the lower deck from the original pack stand-
ing for 9, which is formed by one upper bead and four lower beads.
The two bead counters left in the lower deck gives the remainder 2.
| | | Operations Involved
Sub- | Original | | Bead counter | Bead counter
tractor| minuend | Formula | of the | of the
| | | lower deck | upper deck
-----------------------------------------------------------------
1 |1,2,3,4,6,7,8,9.| -1 = -1 | -1 |
2 |2,3,4,7,8,9. | -2 = -2 | -2 |
3 |3,4,8,9. | -3 = -3 | -3 |
4 |4,9. | -4 = -4 | -4 |
5 |5,6,7,8,9. | -5 = -5 | | -1
6 |6,7,8,9. | -6 = -6 | -1 | -1
7 |7,8,9. | -7 = -7 | -2 | -1
8 |8,9. | -8 = -8 | -3 | -1
9 |9. | -9 = -9 | -4 | -1
Example: 999,999,999 - 123,456,789 = 876,543,210
11
SUBTRACTION
2. COMBINED ADDING-UP AND TAKING-OFF - This
technique is called for when the number of bead counters in the
lower deck is smaller than the subtracter, as in the case of 7-4. To
carry out this operation, one has to add up 1 in the lower deck and
take off 5 (one upper bead counter) in the upper deck, which
means an actual reduction of 4, and gives the correct remainder 3.
| | | Operations Involved
Sub- | Original | | Bead counter | Bead counter
tractor| minuend | Formula | of the | of the
| | | lower deck | upper deck
-----------------------------------------------------------------
1 |5. | -1 = +4-5 | +4 | -1
2 |5,6. | -2 = +3-5 | +3 | -1
3 |5,6,7. | -3 = +2-5 | +2 | -1
4 |5,6,7,8. | -4 = +1-5 | +1 | -1
Example: 5,555,876 - 4,321,432 = 1,234,444
12
SUBTRACTION
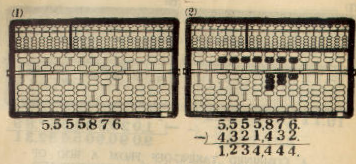
3. TAKING-OFF FROM A ROD OF HIGHER ORDER
AND ADDING-UP - This is called for when the number on a
certain rod is smaller than the supposed subtrahend as in the case
of 13-4. To carry out this operation, one has to take off the one
bead counter from the rod for the order of tens, move one bead
counter up in the lower deck, and move down one bead counter
in the upper deck, which means an actual reduction of 4, and
gives the correct remainder 9.
| | | Operations Involved
Sub- | Original | |Bead counter of the |Bead counter|Bead counter
tractor| minuend |Formula| the lower deck | of the | of the
| | |one rod to the right| lower deck | upper deck
-------------------------------------------------------------------------------
1 |0. |-1=10+9| -1 | +4 | +1
2 |0,1. |-2=10+8| -1 | +3 | +1
3 |0,1,2. |-3=10+7| -1 | +2 | +1
4 |0,1,2,3. |-4=10+6| -1 | +1 | +1
5 |0,1,2,3,4. |-5=10+5| -1 | | +1
6 |0,5. |-6=10+4| -1 | +4 |
7 |0,1,5,6. |-7=10+3| -1 | +3 |
8 |0,1,2,5,6,7. |-8=10+2| -1 | +2 |
9 |0,1,2,3,5,6,7,8|-9=10+1| -1 | +1 |
Example: 10,111,210,200.20 - 1,020,304,567.89 = 9,090,905,632.31
13
SUBTRACTION
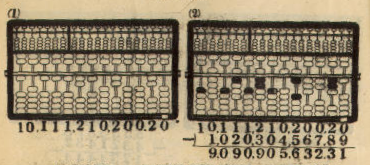
4. COMBINED TAKING-OFF FROM A ROD OF
HIGHER ORDER, ADDING-UP IN THE UPPER DECK AND
TAKING-OFF IN THE LOWER DECK - This technique is call-
ed for when the number on a certain rod is smaller than the
supposed subtrahend, but only in such cases as may be exempli-
fied by 12-6. To carry out this subtraction, one takes off one bead
counter in the upper deck, and again takes off one bead counter
in the lower deck, leaving the number 6 on the unit rod, which is
the required answer. That this is correct can be confirmed by the
fact that the algebraic sum resulted from the operation performed
as above is 6, the subtracter.
| | | Operations Involved
Sub- |Original| |Bead counter of the |Bead counter|Bead counter
tractor|minuend | Formula | the lower deck | of the | of the
| | |one rod to the right| lower deck | upper deck
-----------------------------------------------------------------------------
6 |1,2,3,4.|-6 = -10+5-1| -1 | -1 | +1
7 |2,3,4. |-7 = -10+5-2| -1 | -2 | +1
8 |3,4. |-8 = -10+5-3| -1 | -3 | +1
9 |4. |-9 = -10+5-4| -1 | -4 | +1
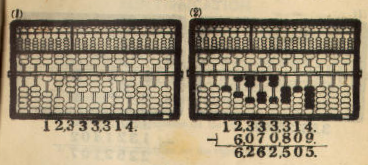
Example: 12,333,314 - 6,070,809 = 6,262,505
14
SUBTRACTION
To carry out a series of subtractions it is obviously easier to
use an abacus than to make the calculations on paper.
The actual procedures can be shown as follows:
Original minuend
+) 1st subtracter
--------------------
1st remainder
+) 2nd subtracter
--------------------
2nd remainder
+) 3rd subtracter
--------------------
3rd remainder
+) 4th subtracter
--------------------
..............
..............
..............
--------------------
(n-1)th remainder
+) nth subtracter
--------------------
nth remainder (Final result)
Example: 3,573,509 - 1,321,402 - 443,086-693,715 = 1,115,306
15
SUBTRACTION
The user must have noticed that in carrying out additions and
subtractions, one does not have to use the two auxiliary operation
fields at all.
16
CHAPTER 4.
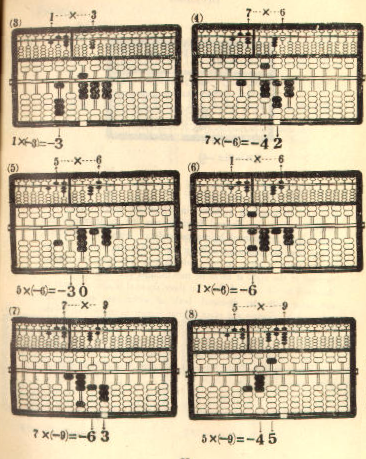
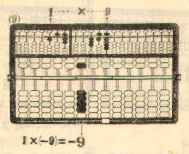
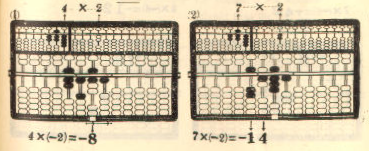
MULTIPLICATION
The method of multiplication on the Lee's abacus is similar
to the method used in ordinary arithmetic, except for the fact that
it can be carried out more rapidly, once the user gets use to it.
To carry out the operations for multiplication, one should
follow carefully the steps prescribed below:
1. Register the multiplicand on the left A-O field.
2. Register the multiplier on the right A-O field.
3. Turn the place setting vernier of the P-O field so as to
have the red dot fall between any two rods convenient for the
operations. Move the indicator to a place immediately under the
red dot.
4. Multiply the digits on the left A-O field, rod by rod, in a
right-to-left order by the right-end digit on the right A-O field,
and register the products one after another on the P-O field as in
carrying out the operations for addition. Be careful, however, not
to place the bead counters on wrong rods, and always remember
to move one-rod to the left in registering the next product. The
indicator should be consulted as a reliable guide for placement.
5. Use the second digit from right on the right A-O field
as multiplier to operate on the digits registered on the left A-O
field, rod by rod, in a right-to-left order, and register the products
on the P-O field one after another as in carrying out operations
for addition. To avoid misplacing bead counters, move the
indicator one rod to the left before adding up the products.
17
MULTIPLICATION
6. Use the third digit from right on the right A-O field as
multiplier to operate on the digits registered on the left A-O field
as before. Remember to move the indicator one rod to the left to
avoid misplacing.
7. Continue the operations as above until every digit on the
right A-O field has been used once.
8. The final reading on the P-O field gives the required
product, and the place setting vernier now indicates the correct
places for all digits.
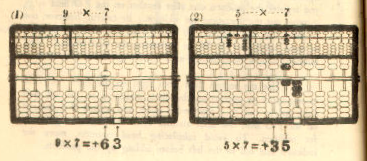
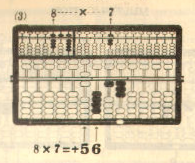
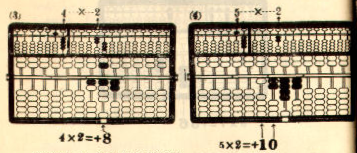
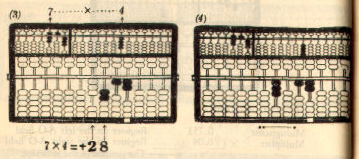
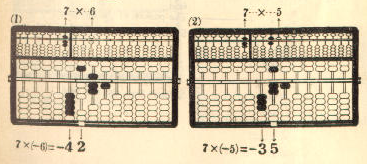
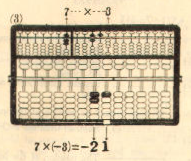
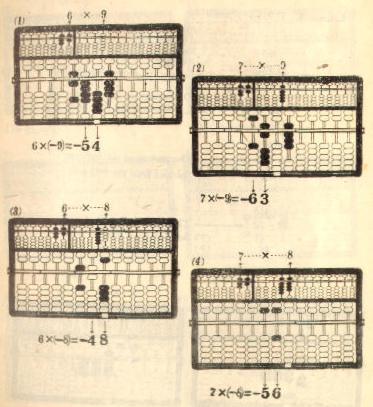
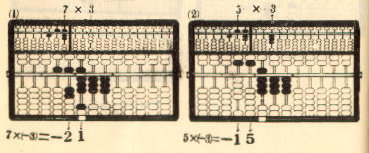
Example 1. 859 x 7 = 6,013
Multiplicand 859 ...... Register on the left A-O field
Multiplier x) 7 ...... Register on the right A-O field
-------------
. <---- The position of the indicator
(9*7) 63 .. (1) Add on the P-O field
(50*7) 35 .. (2) "
(800*7) +) 56 .. (3) "
-------------
Product 6,013 The required product
=============
18
MULTIPLICATION
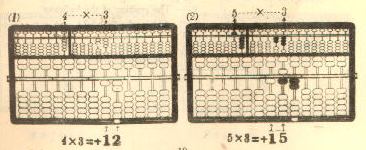
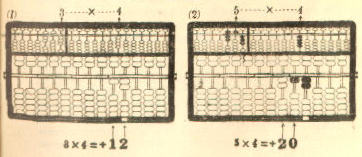
Example 2. 54 x 23 = 1,242
Multiplicand 54 ...... Register on the left A-O field
Multiplier x) 23 ...... Register on the right A-O field
-------------
. <---- The position of the indicator
(4x3) 12 .. (1) Add on the P-O field
(50x3) 15 .. (2) "
. <---- The position of the indicator
(4x20) 8 .. (3) Add on the P-O field
(50x20) +) 10 .. (4) "
-------------
Product 1,242 ...... The required product
=============
19
MULTIPLICATION
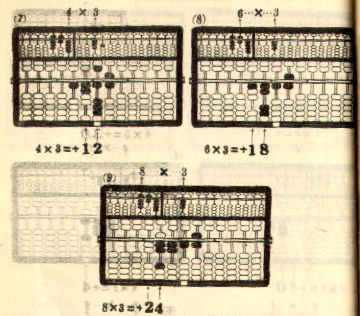
Example 3. 864 x 315 = 272,160
Multiplicand 864 ...... Register on the left A-O field
Multiplier x) 315 ...... Register on the right A-O field
---------------
. <---- The position of the indicator
(4x5) 20 .. (1) Add on the P-O field
(60x5) 30 .. (2) "
(800x5) 40 .. (3) "
. <---- The position of the indicator
(4x10) 4 .. (4) Add on the P-O field
(60x10) 6 .. (5) "
(800x10) 8 .. (6) "
. <---- The position of the indicator
(4x300) 12 .. (7) Add on the P-O field
(60x300) 18 .. (8) "
(800x300) +) 24 .. (9) "
---------------
Product 272,160 ...... The required product
===============
20
MULTIPLICATION
21
MULTIPLICATION
9. When decimal fractions occur in the multiplier or the
multiplicand, or both, whether they are of the improper or the
proper kind, the procedures to follow are just the same as with
integrals. However, special attention should be paid to the dif-
ferent handling of the indicator throughout the operations. If the
right-end digit on the right A-O field is in the order of tenths, then
set the indicator one-rod to the right of the red dot on the vernier,
and move it one-rod each to the left as one goes on dealing with
different digits on the right A-O field in the way prescribed above.
If the right-end digit is in the order of hundredths, then set the
22
MULTIPLICATION
indicator two-rod to the right of the red dot on the vernier before
going ahead with the operations. The user may rely on the same
reasoning in setting the indicator when there should be multipliers
having decimal fractions containing more than three decimal places.
After all products have been properly registered on the P-O field,
the red dot on the place setting vernier - now used as the decimal
point - should be moved one-rod to the left, provided that the
original multiplicand contains a decimal fraction of one decimal
place. It should be move two-rod to the left, provided that the
multiplicand contains a decimal fraction of two decimal places.
The user may apply the same reasoning to deal with multiplicands
containing decimal fractions of more than three decimal places.
The final reading on the P-O field as qualified by the place setting
vernier will be the answer required.
Example 1. 26.5 x 3.4 = 90.1
Multiplicand 26.5 ...... Register on the left A-O field
Multiplier x) 3.4 ...... Register on the right A-O field
---------------
. <----- The position of the indicator
(0.5x0.4) 20 .. (1) Add on the P-O field
(6x0.4) 24 .. (2) "
(20x0.4) 8 .. (3) "
. <----- The position of the indicator
(0.5x3) 15 .. (4) Add on the P-O field
(6x3) 18 .. (5) "
(20x3) +) 6 .. (6) "
---------------
Product 901.0 .. (7) Move the red dot on the place
setting vernier one-rod to the left
90.10 ...... The required product
==============
23
MULTIPLICATION
24
MULTIPLICATION
Example 2. 0.753 x 0.04 = 0.03012
Multiplicand 0.753 ...... Register on the left A-O field
Multiplier x) 0.04 ...... Register on the right A-O field
----------------
. <------The position of the indicator
(0.003x0.04) 12 .. (1) Add on the P-O field
(0.05x0.04) 20 .. (2) "
(0.7x0.04) +) 28 .. (3) "
----------------
Product 0030.12
.<-. .. (4) Move the red dot on the place
setting vernier three-rod to the
left
0.03012 ...... The required product
===============
25
MULTIPLICATION
26
CHAPTER 5.
DIVISION
The method of division on Lee's abacus is also based on
the same principle as that for finding quotients in ordinary arith-
metic. However, the former has been found less strenuous than
the latter. To carry out operations of division, one must be
thoroughly familiar with the operations of subtraction which are
fundamental to the work.
The following steps are to be followed carefully:
1. Move the place setting vernier so as to have the red dot
fall between any two rods on the P-O field, taking into considera-
tion the number of digits in the dividend.
2. Place the dividend properly on the P-O field.
3. Place the divisor properly on the left A-O field.
4. When there is only one digit in the divisor, then set the
indicator right under the rod representing the place of the highest
order in the dividend. Should the digit registered on this rod be
smaller than the divisor, then move the indicator one-rod to the
right to allow two digits to be operated upon. When the divisor
contains two digits, set the indicator under the rod representing
the place of the second highest order in the dividend. Should
the number formed by the digits registered on the two left-end
rods be smaller than the divisor, then move the indicator one more
rod to the right to allow three digits to be operated upon. By the
same reasoning the user will have no difficulty in placing the
indicator correctly when the divisor contains more than three
digits.
27
DIVISION
5. The place order the indicator shows on the P-O field is
to be understood as the highest place order the quotient may have,
i.e., when the indicator comes under the unit rod the quotient must
be a number under 10; when the indicator comes under the rod
representing the order of tens, the quotient then must be under
100; etc.
6. The quotient is to be found digit by digit. Whenever
one digit of the quotient is found, it should be registered on the
right A-O field in accordance with the place order suggested by
the indicator on the P-O field, and the product obtained by
multiplying this digit of the quotient to the divisor should be used
as a subtrahend to be deduced from the dividend on the P-O field.
7. Special attention should be paid to the fact that the digit
of the lowest order in the product falls exactly where the indicator
is as the latter moves along throughout the process of the
operations.
8. In subtracting the product of the quotient and the divisor
from the dividend, the same procedures should be followed as in
carrying out the operations for multiplication, except that all
operations of addition should now be replaced by operations of sub-
traction.
9. After the subtraction is made, one can then proceed to
find the next digit in the quotient. The procedures to follow are
exactly the same as in finding the first digit of the quotient.
10. Repeat the procedures until the dividend on the P-O
field is exhausted. The number represented by the bead counters
on the right A-0 field should be the quotient in question.
28
DIVISION
Example 1. 4,571 / 7 = 653
........................... Register the divisor on the left
: A-O field
: 653 ............ Register the quotient on the right
: ________________ A-O field
-> 7) 4,571 ............ Register the dividend on the P-O
field
. <----------- The position of the indicator
-) 42 ........ (1) Subtract from the P-O field
---------------
371
. <----------- The position of the indicator
-) 35 ........ (2) Subtract from the P-O field
---------------
21
. <----------- The position of the indicator
-) 21 ........ (3) Subtract from the P-O field
---------------
0
=====
29
DIVISION
Example 2. 7,448 / 76 = 98
........................... Register the divisor on the left
: A-O field
: 98 ............ Register the quotient on the right
: ________________ A-O field
-> 76) 7,448 ............ Register the dividend on the P-O
field
. <----------- The position of the indicator
54 ........ (1) Subtract from the P-O field
-) 63 ........ (2) "
---------------
608
. <----------- The position of the indicator
48 ........ (3) Subtract from the P-O field
-) 56 ........ (4) "
---------------
0
=====
30
DIVISION
31
DIVISION
Example 3. 57,933 / 157 = 369
............................. Register the divisor on the left
: A-O field
: 369 ............ Register the quotient on the right
: _________________ A-O field
-> 157) 57,933 ............ Register the dividend on the P-O
field
. <----------- The position of the indicator
21 ........ (1) Subtract from the P-O field
15 ........ (2) "
-)3 ........ (3) "
----------------
10,833
. <----------- The position of the indicator
42 ........ (4) Subtract from the P-O field
30 ........ (5) "
-) 6 ........ (6) "
----------------
1,413
. <----------- The position of the indicator
63 ........ (7) Subtract from the P-O field
45 ........ (8) "
-) 9 ........ (9) "
---------------
0
=====
32
DIVISION
33
DIVISION
11. In handling problems in which the divisor is a
proper or improper decimal fraction, one has to transform the
divisor into an integral before proceeding with the operations.
To do this, one simply has to move the place setting vernier one-rod
to the right if there be only one decimal place in the divisor,
two-rod to the right if there be two decimal places in the divisor,
three-rod to the right if there be three decimal places, etc, and do
the same with the dividend, both of which are automatically
achieved by moving the place setting vernier as many rods to the
right in the P-O field as there a re decimal places in the divisor.
12. After the decimal point in the divisor is removed, the
operations for finding the quotient may then be carried out in the
same way as prescribed above.
34
DIVISION
Example 1. 72.61 / 2.74 = 26.5
______________
2.74) 72.61 Move the red dot on the place
-> -> setting vernier two-rod to the
right
............................. Register the divisor on the left
: A-O field
: 26.5 ........... Register the quotient on the right
: _________________ A-O field
-> 274) 7,261 ........... Register the dividend on the P-O
field
. <---------- The position of the indicator
8 ....... (1) Subtract from the P-O field
14 ....... (2) "
-) 4 ....... (3) "
----------------
1,781
. <---------- The position of the indicator
24 ....... (4) Subtract from the P-O field
42 ....... (5) "
-) 12 ....... (6) "
------------------
137.0
. <---------- The position of the indicator
20 ....... (7) Subtract from the P-O field
35 ....... (8) "
-) 10 ....... (9) "
------------------
0
=====
35
DIVISION
36
DIVISION
37
DIVISION
38
DIVISION
39
DIVISION
40
DIVISION
41
DIVISION
42
CHAPTER 6.
EXTRACTION OF SQUARE ROOTS
To extract square roots on the Lee's abacus is much simpler
job than to do it on paper. The steps to follow are set forth
below:
1. Divide all digits of the square number into groups contain-
ing two digits each. In doing this, start from the decimal point
toward the right for the decimal fraction part and toward the left
for the integral part. Consider it a group by itself even when
there is only one digit at the left-end. But, when there is only
one digit left at the right-end of the decimal fraction part, "0"
shall be supplemented to complete the two digit group.
2. For each group in the square number there will be one
digit in the root to be found. There are, therefore, as many
digits in the square root as there are groups in the square number.
By examining the grouping of the square number, one can tell
of what place order the first digit of the root will be.
3. Before starting to operate, the place setting vernier should
be turned to a position most convenient for the calculation.
4. Register the square number on the P-O field in reference
to the place setting vernier.
5. Move the indicator to mark out the first group from the
left.
6. When the square number has only one group for the
integral part, the root must be a number under 10. When there
are two groups for the integral part of the square number, the root
must be a number less than 100. When there are three groups
43
EXTRACTION OF SQUARE ROOTS
in the square number, there must also be three integral places in
the square root. The same reasoning hold good for all cases.
7. In making the calculation, first add one bead counter up
in the left A-O field in accordance with the placement suggested
by the indicator, and subtract 1 from the first group in the P-O
field.
8. Secondly, add 2 to the original 1 on the left A-O field,
and subtract the sum 3 from the first group on the P-O field; add
2 again to the original 3 on the left A-O field, and subtract the
sum 5 from the first group on the P-O field; add 2 again to the
original 5 on the left A-O field, and subtract the sum 7 from the
first group on the P-O field; - repeat these operations until the
remainder of the first group becomes smaller than the sum on the
left A-O field.
9. Thirdly, add up one bead counter each to the first and
the second digit from the left on the left A-O field (symbol 1.1
will be used hereafter), move the indicator two-rod to the right,
and subtract the sum on the left A-O field from the number
formed by the first and the second group of the square number.
There may be cases when nothing is left on the first group. In
such cases, just subtract the sum on the left A-O field from the
number formed by the second group alone.
10. Fourthly, add 2 to the left A-O field, and subtract the
sum from the P-O field; add 2 again to the left A-O field, and
subtract the sum from the P-O field; and so on until the remainder
of the second group on the P-O field becomes smaller than the
sum on the left A-O field.
44
EXTRACTION OF SQUARE ROOTS
11. Repeat the operations described in Items 9 and 10 when
necessary.
12. Fifthly, when all bead counters on the P-O field have
been taken off the beam as a result of the operations, add 1 to the
sum on the left A-O field and divide it up by 2. The quotient
thus obtained is the root required.
13. There may be cases when the remainder in the P-O
field is inexhaustible. This means that the original number on
which the operations of root extraction is made is not a perfect
square number. Even so, the root obtained by carrying out the
operations described in Item 12 gives a good approximation.
___________
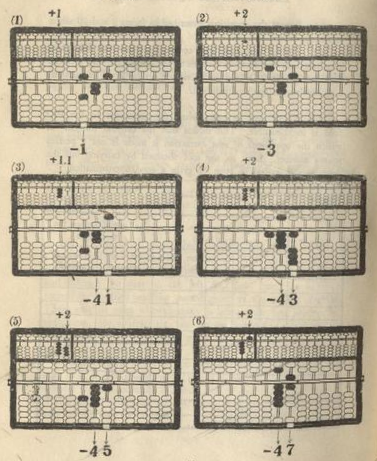
Example: V 625 = 25
| "+" operations on the | "-" operations on the
Figure | left A-O field | P-O field
No | | | | 1st | 2nd | First | Second
| | | |digit|digit| group | group
-----------------------------------------------------------
1 | | | | 1 | | | 1 | |
2 | | | | 2 | | | 3 | |
3 | | | | 1 | 1 | | | 4 | 1
4 | | | | | 2 | | | 4 | 3
5 | | | | | 2 | | | 4 | 5
6 | | | | | 2 | | | 4 | 7
7 | | | | | 2 | | | 4 | 9
| + 4 9 | - 6 2 5
| |
8 | 49 + 1 = 50
9-10 | 50 / 2 = 25
45
EXTRACTION OF SQUARE ROOTS
46
EXTRACTION OF SQUARE ROOTS
14. In carrying out the operations described in Item 9 above,
if the minuend in the P-O field is still smaller than the sum in
the left A-O field after having gone through the procedures of
adding 1.1 to the left A-O field and moving the indicator two-rod
to the right on the P-O field, one has then to move the indicator
two-rod more to the right, and add 1.01 instead of 1.1 to the left
A-O field.
47
EXTRACTION OF SQUARE ROOTS
___________
Example: V 1,664.64 = 40.8
| "+" operations |
Operation | on the left | "-" operations on the
Procedures| A-O field | P-O field
| 1st | 2nd | 3rd | First | Second | Third
| digit | digit | digit | group | group | group
--------------------------------------------------------------------
1 | 1 | | | | 1 | | | |
2 | 2 | | | | 3 | | | |
3 | 2 | | | | 5 | | | |
4 | 2 | | | | 7 | | | |
5 | 1 | 0 | 1 | | | 0 | 8 | 0 | 1
6 | | | 2 | | | | 8 | 0 | 3
7 | | | 2 | | | | 8 | 0 | 5
8 | | | 2 | | | | 8 | 0 | 7
9 | | | 2 | | | | 8 | 0 | 9
10 | | | 2 | | | | 8 | 1 | 1
11 | | | 2 | | | | 8 | 1 | 3
12 | | | 2 | | | | 8 | 1 | 5
| + 8 1 . 5 |- 1 , 6 6 4 . 6 4
| |
13 | 81.5 + 0.1 = 81.6
14-15 | 81.6 / 2 = 40.8
15. After having followed the prescriptions in Item 14, the
minuend in the P-O field may still be smaller than the sum in the
left A-O field. In such cases, the indicator should be moved
again two-rod tow the right and, instead of 1.1 or 1.01, the number
to be added to the left A-O field should then be 1.001. The same
reasoning applies to all cases of similar nature.
48
EXTRACTION OF SQUARE ROOTS
___________
Example: V 1,004,004 = 1,002
| "+" operations on the | "-" operations on the
Operation | left A-O field | P-O field
Procedures| 1st | 2nd | 3rd | 4th | First | Second | Third | Fourth
|digit|digit|digit|digit| group | group | group | group
---------------------------------------------------------------------------
1 | 1 | | | | | 1 | | | | | |
2 | 1 | 0 | 0 | 1 | | | 0 | 0 | 2 | 0 | 0 | 1
3 | | | | 2 | | | | | 2 | 0 | 0 | 3
|+ 2 , 0 0 3 | - 1 , 0 0 4 , 0 0 4
| |
4 | 2,003 + 1 = 2,004
5-6 | 2,004 / 2 = 1,002
49
EXTRACTION OF CUBIC ROOTS
The operations involved in finding cubic roots on the Lee's
abacus are but those of additions and subtractions. To extract
cubic roots, follow the steps set forth below:
1. Divide all digits of the cubic number into groups of three
digits each. In doing this, start from the decimal point toward
the right for the decimal fraction part and toward the left for the
integral part. Consider it a group by itself even when there is
only one, or two, digits left at the right-end of the decimal
fraction part, "0" must be supplemented to make the group con-
tain three digits.
2. For each group in the cubic number, there will be one
digit in the root to be found. There are, therefore, as many digits
in the cubic root as there are groups in the cubic number. By
examining the grouping of the cubic number, one can tell of what
place order the first digit of the root will be.
3. Before starting to operate, the place setting vernier should
be turned to a position most convenient for the calculation.
4. Register the cubic number on the P-O field in reference
to the place setting vernier.
5. Move the indicator to mark out the first group from the
left.
6. When the cubic number has only one group for the
integral part, the root must be a number less than 10. When
there are two groups for the integral part of the cubic number, the
51
EXTRACTION OF CUBIC ROOTS
root must be a number under 100. When there are three groups
for the integral part of the cubic number, the root must then be a
number under 1,000. The same reasoning holds good for all cases.
7. In making the calculation, first add one bead counter up
to the left A-O field in accordance with the placement suggested
by the indicator (hereafter referred to as "L-number"), add one
bead counter up to the right A-O field (hereafter referred to as
"R-number"), and then subtract 1 from the first group on the
P-O field.
8. Secondly, add 1 to the L-number, add the resultant L-
number to the R-number, add 2 to the L-number, add the resultant
L-number (4) to the R-number, and subtract the resultant R-
number (7) from the first group on the P-O field. Then, add 1
to the L-number, add the resultant L-number to the R-number,
add 2 to the L-number, add the resultant L-number to the R-
number, and subtract the resultant R-number from the first group
on the P-O field. Repeat these operations until the remainder
of the first group of the cubic number becomes smaller than the
corresponding R-number.
9. Thirdly, add 1 to the L-number and add the resultant
L-number to the R-number.
10. Fourthly, add up one bead counter each to the first and
the second digit from the left of the L-number (symbol 1.1 will
be used hereafter) add the resultant L-number to the R-number,
lowering the place order of the former by "two" in this addition,
move the indicator three-rod to the right, and then subtract the
R-number from the number formed by the first and the second
group of the cubic number.
52
EXTRACTION OF CUBIC ROOTS
11. Fifthly, add 1 to the second digit of the L-number, add
the resultant L-number to the R-number, add 2 to the second digit
of the L-number, add the resultant L-number to the R-number,
subtract the resultant R-number from the second group of the cubic
number on the P-O field. Repeat these operations until the
remainder of the second group of the cubic number on the P-O
field becomes smaller than the corresponding R-number.
12. Continue the operations described in Items 10 and 11
when necessary.
13. Sixthly, when all bead counters in the P-O field have
been taken off the beam as a result of the operations, add 2 to the
L-number and divide it up by 3. The quotient thus obtained will
be the root required.
3_____________
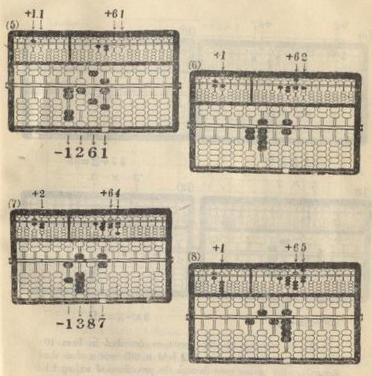
Example: V 12,167 = 23
|"+" operations on the | "+" operations on the | "-" operations on
| left A-O field | right A-O field | the P-O
Figure | (L-number) | (R-number) | field
No. | | 1st | 2nd | Order | Order | First | Second
| | digit | digit | 1 | 2 | group | group
---------------------------------------------------------------------------
1 | | 1 | | | 1 | | | | | 1 | | |
2 | | 1 | | | 2 | | | | | | | |
3 | | 2 | | | 4 | | | | | 7 | | |
4 | | 1 | | | 5 | | | | | | | |
5 | | 1 | 1 | | | 6 | 1 | | | 1 | 2 | 6 | 1
6 | | | 1 | | | 6 | 2 | | | | | |
7 | | | 2 | | | 6 | 4 | | | 1 | 3 | 8 | 7
8 | | | 1 | | | 6 | 5 | | | | | |
9 | | | 2 | | | 6 | 7 | | | 1 | 5 | 1 | 9
| + 6 7 | | - 1 2 , 1 6 7
| | |
10 | 67 + 2 = 69
11-12| 69 / 3 = 23
53
EXTRACTION OF CUBIC ROOTS
54
EXTRACTION OF CUBIC ROOTS
55
EXTRACTION OF CUBIC ROOTS
14. In carrying out the operations described in Item 10
above, if the minuend in the P-O field is still smaller than the
R-number after having gone through the procedures of adding 1.1
to he L-number and moving the indicator three rods to the right
on the P-O field, one has then to move the indicator three-rod more
to the right, add 1.01 instead of 1.1 to the L-number, and add
the resultant L-number to the R-number, lowering the former's
place order by "four" instead of "two" in this addition.
56
EXTRACTION OF CUBIC ROOTS
3_____________
Example: V 8,615.125 = 20.5
| "+" operations | "+" operations | "-" operations on
Opera- | on the left | on the right | the P-O field
tion | A-O field | A-O field |
Proced-| | 1st | 2nd | 3rd |Order|Order|Order| 1st | 2nd | 3rd
ures | |digit|digit|digit| 1 | 2 | 3 | group | group | group
-----------------------------------------------------------------------------
1 | | 1 | | | |1 | | | | | | |1 | | | | | |
2 | | 1 | | | |2 | | | | | | | | | | | | |
3 | | 2 | | | |4 | | | | | | |7 | | | | | |
4 | | 1 | | | |5 | | | | | | | | | | | | |
5 | | 1 | 0 | 1 | | |0 |6 |0 |1 | | | |1 |2 |0 |6 |0 |1
6 | | | | 1 | | | |6 |0 |2 | | | | | | | | |
7 | | | | 2 | | | |6 |0 |4 | | | |1 |2 |1 |8 |0 |7
8 | | | | 1 | | | |6 |0 |5 | | | | | | | | |
9 | | | | 2 | | | |6 |0 |7 | | | |1 |2 |3 |0 |1 |9
10 | | | | 1 | | | |6 |0 |8 | | | | | | | | |
11 | | | | 2 | | | |6 |1 |0 | | | |1 |2 |4 |2 |3 |7
12 | | | | 1 | | | |6 |1 |1 | | | | | | | | |
13 | | | | 2 | | | |6 |1 |3 | | | |1 |2 |5 |4 |6 |1
| + 6 1 . 3 | | - 8 ,6 1 5 .1 2 5
| | |
14 | 61.3 + 0.2 = 61.5
15-16| 61.5 / 3 = 20.5
15. After having followed the prescriptions in Item 14, the
minuend in the P-O field may still be smaller than the R-number.
In such cases, the indicator should be brought again three-rod more
to the right, and what is supposed to be added to the L-number
should be 1.001 instead of 1.1 or 1.01. When adding the resultant
L-number to the R-number, the former's place order should
then be lowered by "six". The same reasoning holds good for all
cases of similar nature.
57
EXTRACTION OF CUBIC ROOTS
3_____________
Example: V 8,036.054027 = 20.03
Opera- | "+" operations on the | "+" operations on the | "-" operations on the
tion | left A-O field | right A-O field | P-O field
Proced-| | 1st | 2nd | 3rd | 4th |Order|Order|Order|Order| 1st | 2nd | 3rd | 4th
ures | |digit|digit|digit|digit| 1 | 2 | 3 | 4 | group | group | group | group
-------------------------------------------------------------------------------------------------
1 | | 1 | | | | |1 | | | | | | | | |1 | | | | | | | | |
2 | | 1 | | | | |2 | | | | | | | | | | | | | | | | | |
3 | | 2 | | | | |4 | | | | | | | | |7 | | | | | | | | |
4 | | 1 | | | | |5 | | | | | | | | | | | | | | | | | |
5 | | 1 | 0 | 0 | 1 | | |0 |0 |6 |0 |0 |1 | | | | |1 |2 |0 |0 |6 |0 |0 |1
6 | | | | | 1 | | | | |6 |0 |0 |2 | | | | | | | | | | | |
7 | | | | | 2 | | | | |6 |0 |0 |4 | | | | |1 |2 |0 |1 |8 |0 |0 |7
8 | | | | | 1 | | | | |6 |0 |0 |5 | | | | | | | | | | | |
9 | | | | | 2 | | | | |6 |0 |0 |7 | | | | |1 |2 |0 |3 |0 |0 |1 |9
| + 6 0 . 0 7 | | - 8 ,0 3 6 .0 5 4 0 2 7
| | |
10 | 60.07 + 0.02 = 60.09
11-12| 60.09 / 3 = 20.03
16. There may be cases when the remainder in the P-O
field is inexhaustible. This means that the original number on
which the operations of root extraction is made is not a perfect
cubic number. Even so, the root obtained by carrying out the
operations described above makes a good approximation.
58
OCR version of HOW TO LEARN LEE'S ABACUS (58 pages w/ spelling corrections)
The inside cover or title page shows a
JP Left Aux 7 Rail, JP Right Aux 11 Rail, & KO Primary 13 Rail Abacus.
Elsewhere shows a
JP Left Aux 7 Rail, JP Right Aux 13 Rail, & CN Primary 13 Rail Abacus.
Also produced was a
JP Light Green Left Aux 9 Rail, JP White Right Aux 9 Rail, & Black CN Primary 13 Rail Abacus (pictured above: Extra).
Roots are calculated by a variant of Newton's Method.